How to compute length of shaft from hallow shaft torsion. It’s important to note that shear strain and shaft length are inversely proportional: Θ = angle of twist in radians on a length. From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. Torsional strain energy is given as, shaft of varying diameter:
 Torsional Stress From slideshare.net
Torsional Stress From slideshare.net
Maximum moment in a circular shaft can be expressed as: From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. Hollow shaft outer diameter (m) d s: On an element where shear stress is maximum, normal stress is 0. L = length of the shaft. M e = ( π ÷ 32) ∗ σ b ∗ d 3.
Let re and r be the external and internal radius and de and d be the external and internal diameter of the hollow shaft, respectively.
When designing the shaft for the bending moment, we can apply the formula shown: From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. The radius can be calculated by the above equation and shear stress is given as 78mpa by substituting all the above equations we get the radius of the shaft r =0.07196 meters or 71.96. Torsional strain energy is given as, shaft of varying diameter: Maximum moment in a circular shaft can be expressed as: It’s important to note that shear strain and shaft length are inversely proportional:
 Source: studylib.net
Source: studylib.net
M e = ( π ÷ 32) ∗ σ b ∗ d 3. Α = angular shaft deflection. D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. Torsional strain energy is given as, shaft of varying diameter: L = shaft length in m g = shear modulus in n/m 2 (steel is 80·10 9 j = polar moment in m 4 (j = π·r 4 /2 for a solid cylinder) if you solve for radius r, you get about 12 mm;
 Source: chegg.com
Source: chegg.com
D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. Calculations for shear and angle of deflection are. Where σ b = ultimate/allowable stress. Maximum moment in a circular shaft can be expressed as: Hollow shaft outer diameter (m) d s:
 Source: chegg.com
Source: chegg.com
Θ = angle of twist in radians on a length. The longer the shaft, the lower the shear strain. L = length of the shaft. L = shaft length in m g = shear modulus in n/m 2 (steel is 80·10 9 j = polar moment in m 4 (j = π·r 4 /2 for a solid cylinder) if you solve for radius r, you get about 12 mm; Θ = angle of twist in radians on a length.
 Source: slideshare.net
Source: slideshare.net
When designing the shaft for the bending moment, we can apply the formula shown: Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. L = length of the shaft. Α = angular shaft deflection. Hollow shaft outer diameter (m) d s:
 Source: slideshare.net
Source: slideshare.net
Γ = shear strain (radians) r = distance along. Hollow shaft shear stress and angular deflection calculator. Γ = shear strain (radians) r = distance along. Most common torsion problems will indicate the. The longer the shaft, the lower the shear strain.
 Source: chegg.com
Source: chegg.com
It’s important to note that shear strain and shaft length are inversely proportional: To simplify this above calculation process, we can find the least critical shaft diameter by using the following t e formula used for the shaft subjected to fluctuating and. A hollow steel shaft with a diameter ratio of 0.75 and a length of 4 m is required to transmit 1 mw at 120 rev/min. From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is.
 Source: slideshare.net
Source: slideshare.net
From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. Where σ b = ultimate/allowable stress. The maximum shear stress is not to exceed 70 mn/m2 nor is. Hollow shaft outer diameter (m) d s: Maximum moment in a circular shaft can be expressed as:
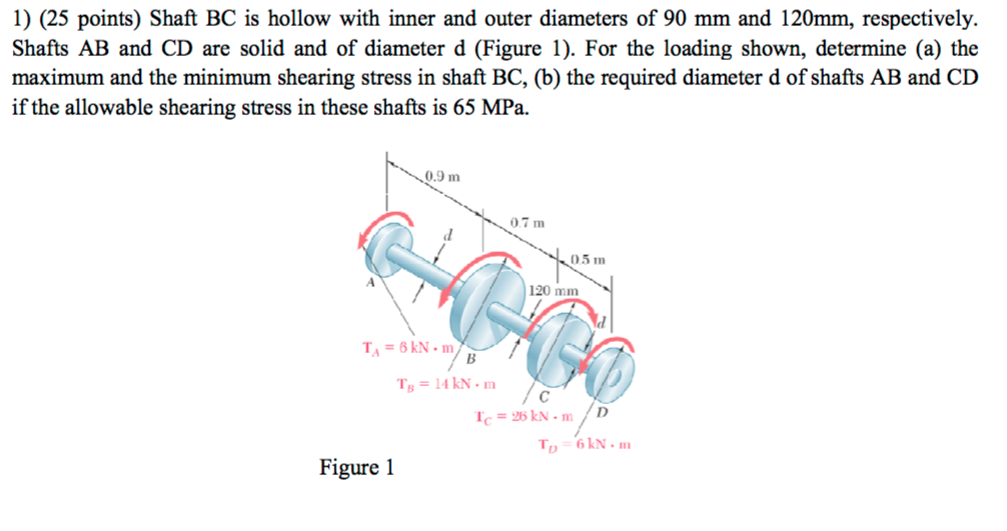 Source: chegg.com
Source: chegg.com
Hollow shaft shear stress and angular deflection calculator. Hollow shaft shear stress and angular deflection calculator. Maximum moment in a circular shaft can be expressed as: L = length of the shaft. Α = angular shaft deflection.

Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. Calculations for shear and angle of deflection are. Α = angular shaft deflection. It’s important to note that shear strain and shaft length are inversely proportional: The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is.
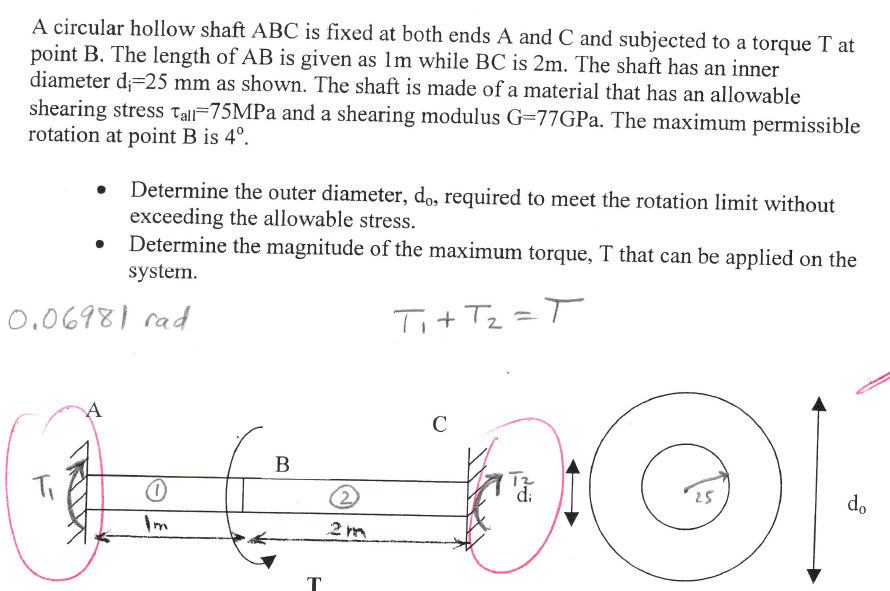 Source: chegg.com
Source: chegg.com
The maximum shear stress is not to exceed 70 mn/m2 nor is. From torsion equation we can consider it can be written as the polar moment of inertia will be calculated. Maximum moment in a circular shaft can be expressed as: Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. Torsional stiffness = t θ t θ from the torsional equation, t θ = gj l t θ = g j l where, g = modulus of rigidity j = polar moment of inertia l = length of shaft therefore torsional.

On an element where shear stress is maximum, normal stress is 0. Torsional stiffness = t θ t θ from the torsional equation, t θ = gj l t θ = g j l where, g = modulus of rigidity j = polar moment of inertia l = length of shaft therefore torsional. Da = 2π rdr (6.16) fig. The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is. Α = angular shaft deflection.
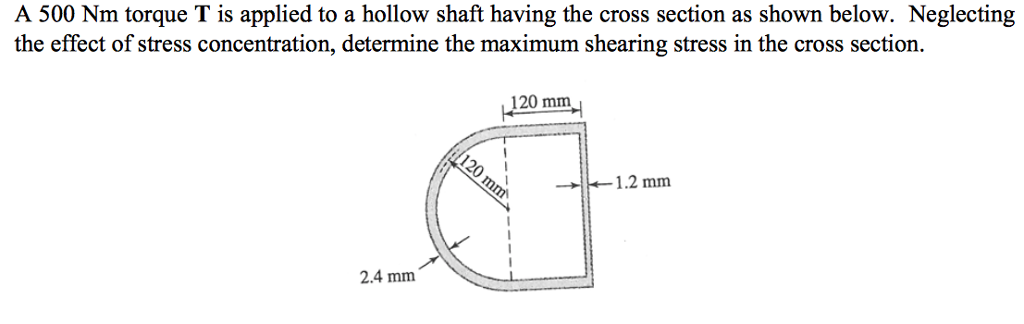 Source: chegg.com
Source: chegg.com
I am currently reviewing a simple hollow shaft extension design which is basically a pipe with a flange at each end under torsion. When designing the shaft for the bending moment, we can apply the formula shown: Torsional stiffness = t θ t θ from the torsional equation, t θ = gj l t θ = g j l where, g = modulus of rigidity j = polar moment of inertia l = length of shaft therefore torsional. L = length of the shaft. The maximum shear stress is not to exceed 70 mn/m2 nor is.
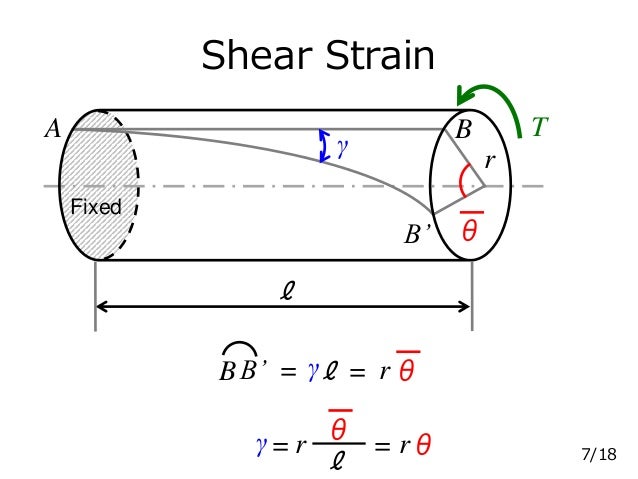 Source: slideshare.net
Source: slideshare.net
The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is. Γ = shear strain (radians) r = distance along. Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. Torsional strain energy is given as, shaft of varying diameter: A hollow steel shaft with a diameter ratio of 0.75 and a length of 4 m is required to transmit 1 mw at 120 rev/min.
 Source: chegg.com
Source: chegg.com
Torsional strain energy is given as, shaft of varying diameter: Hollow shaft shear stress and angular deflection calculator. Solid shaft diameter (m) k: Let re and r be the external and internal radius and de and d be the external and internal diameter of the hollow shaft, respectively. A hollow steel shaft with a diameter ratio of 0.75 and a length of 4 m is required to transmit 1 mw at 120 rev/min.

Da = 2π rdr (6.16) fig. M e = ( π ÷ 32) ∗ σ b ∗ d 3. Shear stress is zero on the axis passing through the center of a shaft and maximum at the outside surface of a shaft. It’s important to note that shear strain and shaft length are inversely proportional: Let re and r be the external and internal radius and de and d be the external and internal diameter of the hollow shaft, respectively.
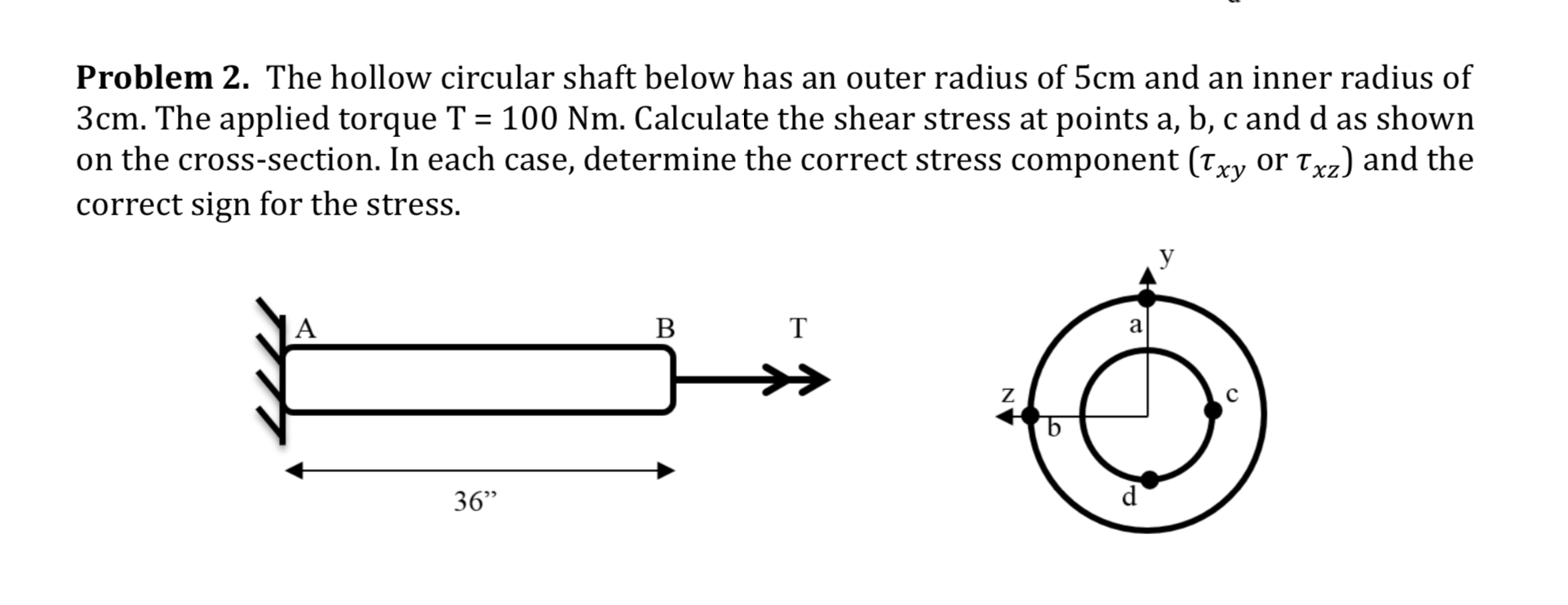 Source: chegg.com
Source: chegg.com
The longer the shaft, the lower the shear strain. Enter moment, diameter and length values, select your material and units as required. D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. Shear stress is zero on the axis passing through the center of a shaft and maximum at the outside surface of a shaft. On an element where shear stress is maximum, normal stress is 0.
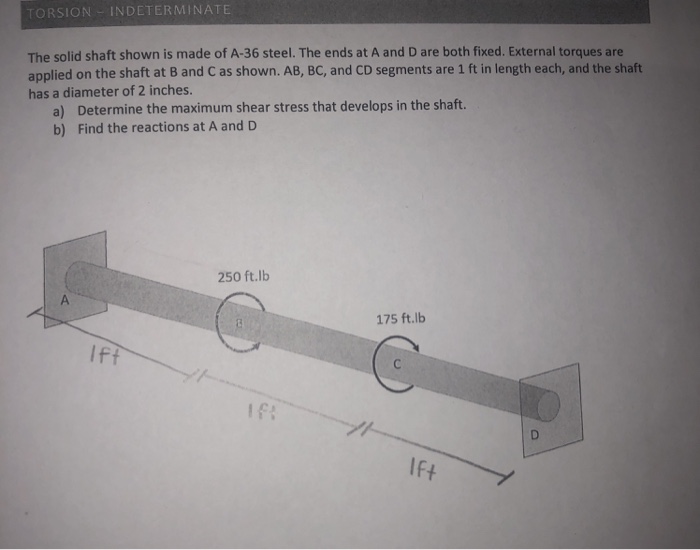
D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. M e = ( π ÷ 32) ∗ σ b ∗ d 3. D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. Θ = angle of twist in radians on a length. To simplify this above calculation process, we can find the least critical shaft diameter by using the following t e formula used for the shaft subjected to fluctuating and.
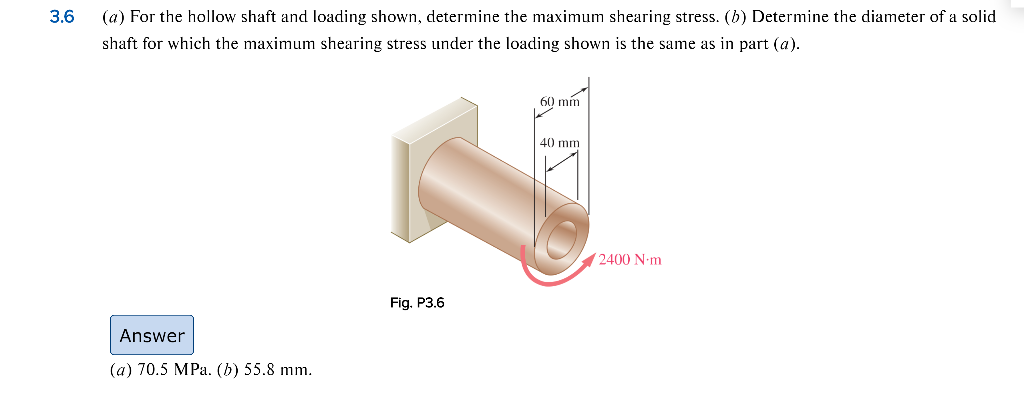 Source: chegg.com
Source: chegg.com
The radius can be calculated by the above equation and shear stress is given as 78mpa by substituting all the above equations we get the radius of the shaft r =0.07196 meters or 71.96. L = length of the shaft. Da = 2π rdr (6.16) fig. I am currently reviewing a simple hollow shaft extension design which is basically a pipe with a flange at each end under torsion. Calculations for shear and angle of deflection are.
 Source: chegg.com
Source: chegg.com
M e = ( π ÷ 32) ∗ σ b ∗ d 3. Da = 2π rdr (6.16) fig. The maximum shear stress is not to exceed 70 mn/m2 nor is. Γ = shear strain (radians) r = distance along. The radius can be calculated by the above equation and shear stress is given as 78mpa by substituting all the above equations we get the radius of the shaft r =0.07196 meters or 71.96.
 Source: chegg.com
Source: chegg.com
Let re and r be the external and internal radius and de and d be the external and internal diameter of the hollow shaft, respectively. M e = ( π ÷ 32) ∗ σ b ∗ d 3. D = outside diameter (mm, in.) d = inside diameter (mm, in.) g =. On an element where shear stress is maximum, normal stress is 0. Θ = angle of twist in radians on a length.
 Source: slideshare.net
Source: slideshare.net
The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is. L = length of the shaft. Torsional stiffness = t θ t θ from the torsional equation, t θ = gj l t θ = g j l where, g = modulus of rigidity j = polar moment of inertia l = length of shaft therefore torsional. On an element where shear stress is maximum, normal stress is 0. Da = 2π rdr (6.16) fig.
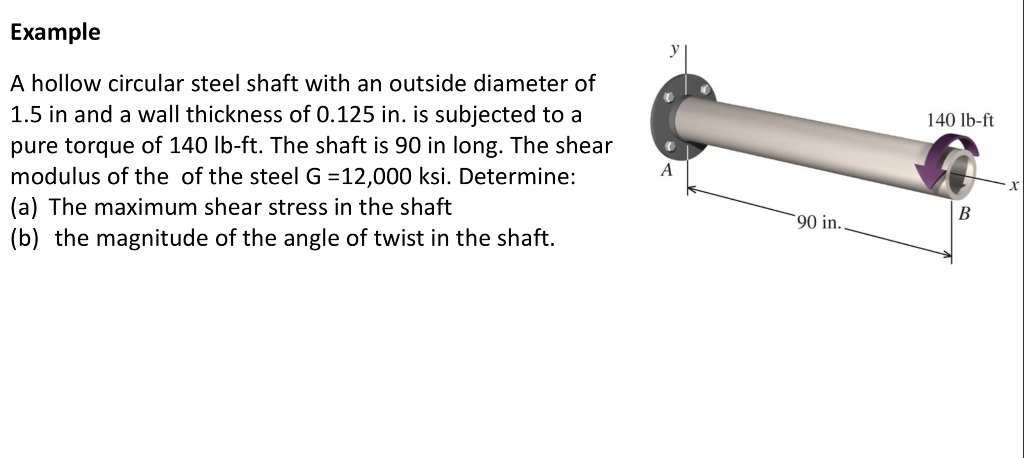 Source: chegg.com
Source: chegg.com
The length of shaft given angle of twist of hollow shaft on basis of torsional rigidity formula is defined as length of the hollow shaft on which we are applying twisting moment and is. Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. The radius can be calculated by the above equation and shear stress is given as 78mpa by substituting all the above equations we get the radius of the shaft r =0.07196 meters or 71.96. L = length of the shaft, [m, in] the nomenclature above follows the same convention as panglobal power engineering training system. To simplify this above calculation process, we can find the least critical shaft diameter by using the following t e formula used for the shaft subjected to fluctuating and.
 Source: chegg.com
Source: chegg.com
Most common torsion problems will indicate the. Tmax = σmax ip / r (2) where tmax = maximum twisting moment (nm, in lb) σmax = maximum shear stress (mpa,. When designing the shaft for the bending moment, we can apply the formula shown: L = length of the shaft, [m, in] the nomenclature above follows the same convention as panglobal power engineering training system. It’s important to note that shear strain and shaft length are inversely proportional:
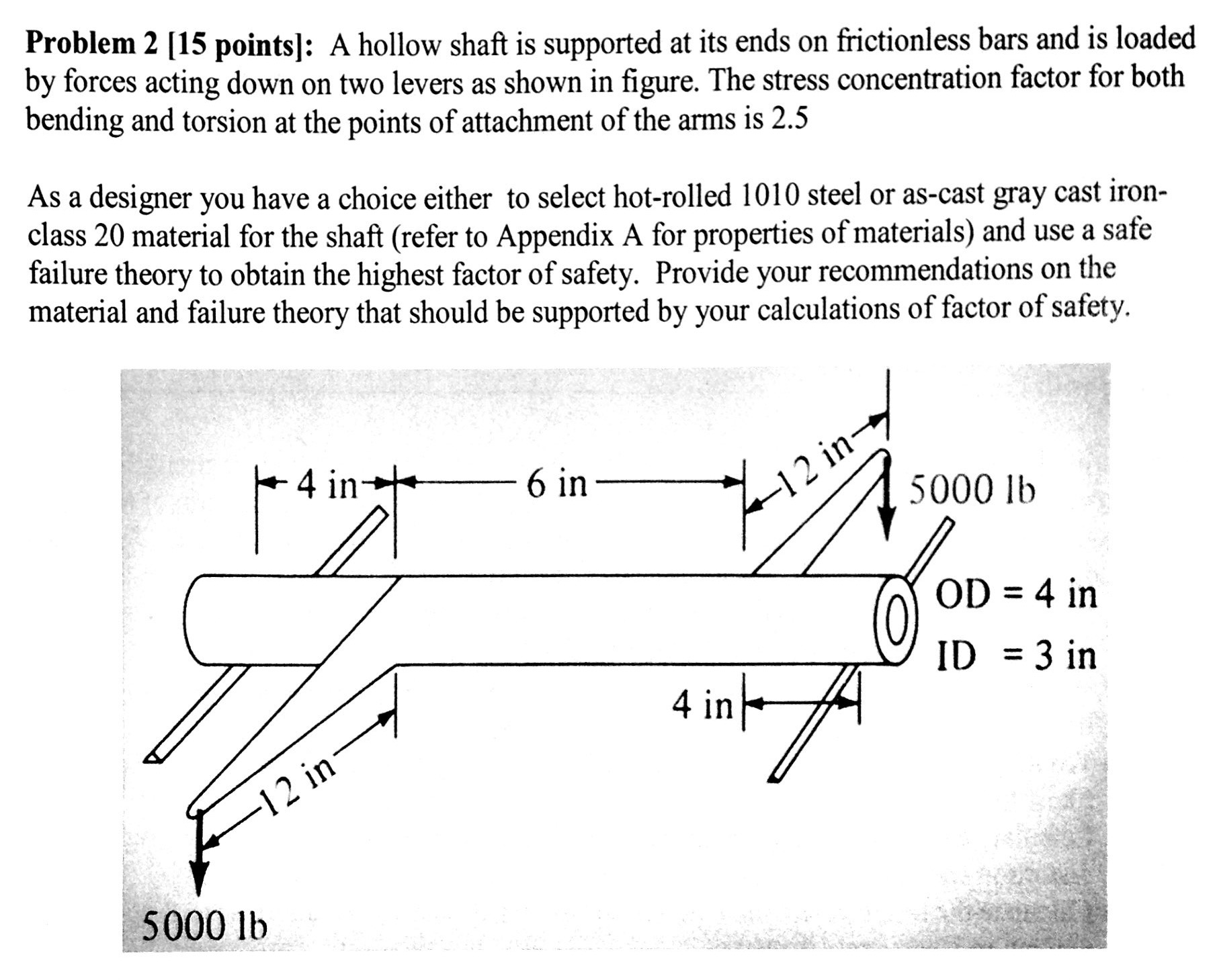 Source: chegg.com
Source: chegg.com
To simplify this above calculation process, we can find the least critical shaft diameter by using the following t e formula used for the shaft subjected to fluctuating and. Α = angular shaft deflection. Γ = shear strain (radians) r = distance along. Where σ b = ultimate/allowable stress. M e = ( π ÷ 32) ∗ σ b ∗ d 3.

Calculations for shear and angle of deflection are. It’s important to note that shear strain and shaft length are inversely proportional: To simplify this above calculation process, we can find the least critical shaft diameter by using the following t e formula used for the shaft subjected to fluctuating and. On an element where shear stress is maximum, normal stress is 0. The radius can be calculated by the above equation and shear stress is given as 78mpa by substituting all the above equations we get the radius of the shaft r =0.07196 meters or 71.96.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title how to compute length of shaft from hallow shaft torsion by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.